パーツモデリングの記事で学んだ内容の練習がしたい！コマンドを組合せたモデリングがしたい！コマンドのほかの使い方が知りたい！と思っていませんか？
パーツモデリングの記事を読めばモデリングのやり方が分かるようになりますが、コマンドを組合せたモデリングをする場合、一連の流れを経験して慣れておく必要があります。
私は機械設計のエンジニアとして仕事をしているので、FreeCADが使えるようになりたくて学習を続けていますが、この記事を執筆する上でいくつもの問題に当たり解決方法を探すのに苦労しました。
そこでこの記事では、練習問題でコマンドを組合せたモデリングからマルチボディのモデリング、計測までをまとめて解説します。
この記事で練習できること。
- 第三角法の図面からモデリング
- マルチボディのモデリング
- 2点間距離と面積、体積、重心座標の計測
この記事は図解でわかりやすく解説しているので、初心者でも手順どおりに進めれば、練習問題のモデリングができます。
コマンドを組合せたモデリングやマルチボディのモデリング、計測を習得したい方は、是非ともこの記事を読んであなたの「ものづくり」に役立ててください。
練習問題
「FreeCADの使い方」の記事から「初期設定」「スケッチ」「Part Design」「パーツモデリング」「アセンブリ」を読んだ方は、学習した内容の定着を図るため練習問題を解いてみてください。
練習問題は資格試験の問題を利用することによって、達成感を得ることもできると考えたので、「3次元CAD利用技術者試験 1級・準1級サンプル問題」を選びました。
このサンプル問題は3次元CAD利用技術者試験の公式サイトから（こちらのサイトの末尾にPDF形式でダウンロードできます）無料でダウンロードできるので、ここからはダウンロードしてあることを前提に解説していきます。
練習問題の構成
問題は問1から問5までありますが、取り掛かりやすい順番に並べ替えています。
最初の問題には図面から立体形状をイメージしやすく、コマンドの使用順序もわかりやすい問5を選びました。（手順もひとつずつ解説していきます）
それ以降の問ではテンポ良く解説するため、問5と同程度の内容を割愛することにしました。
練習問題を解くためのポイント
- 第三角法の図面から立体形状をイメージする
- どの順序でモデリングしていくかザックリと決める
- 原点の位置を確認して、原点を通る形状から作り始める
下記の記事を読むと練習問題のモデリングや計測ができるようになります。
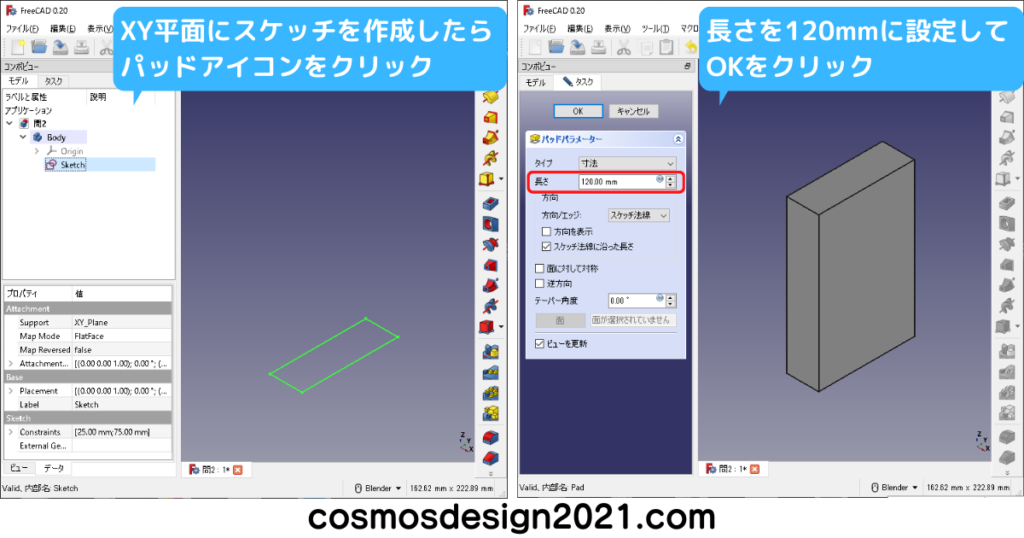
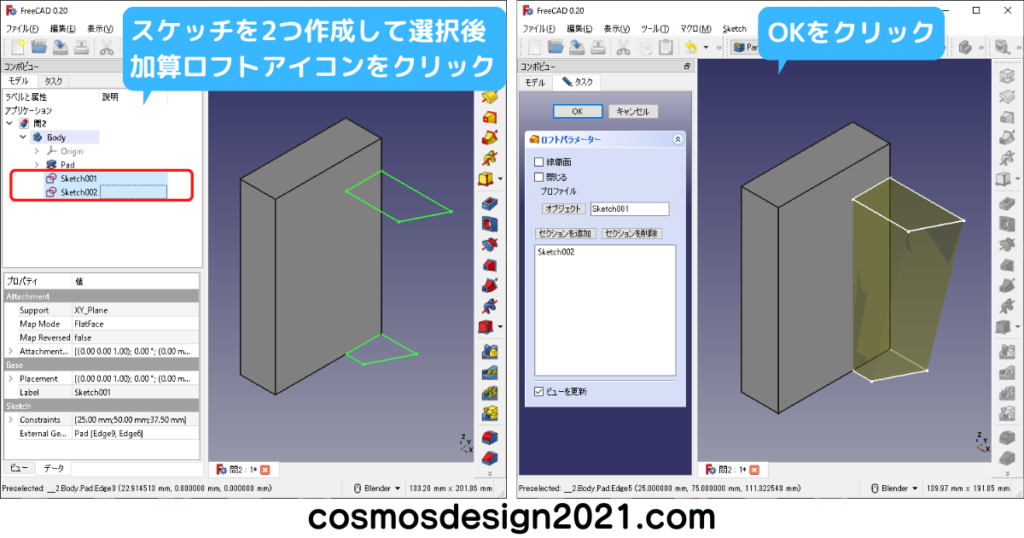
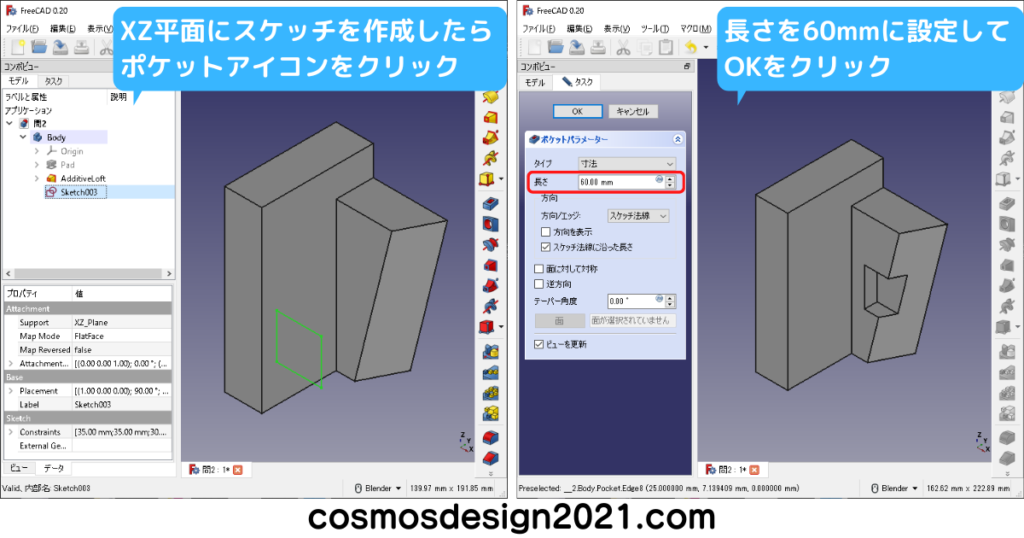
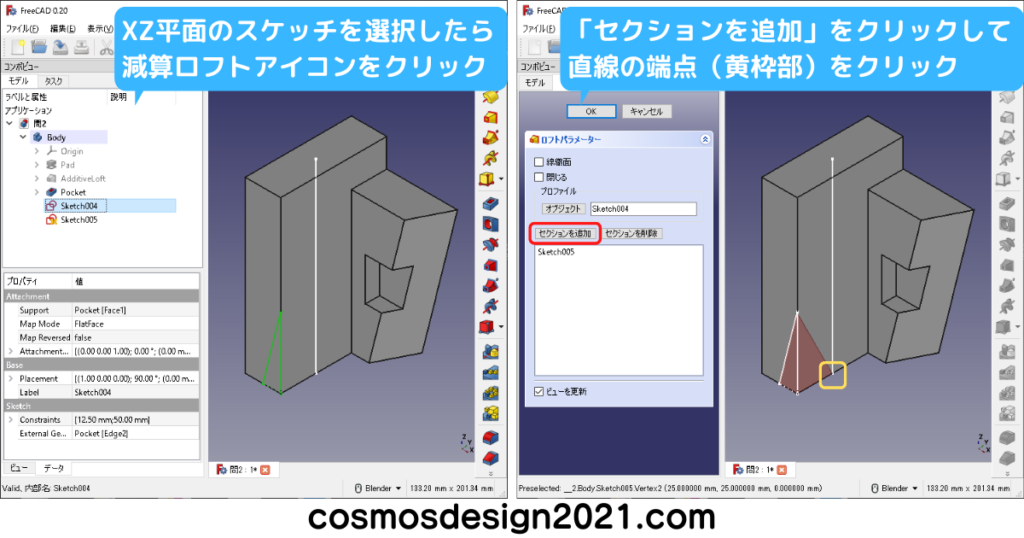
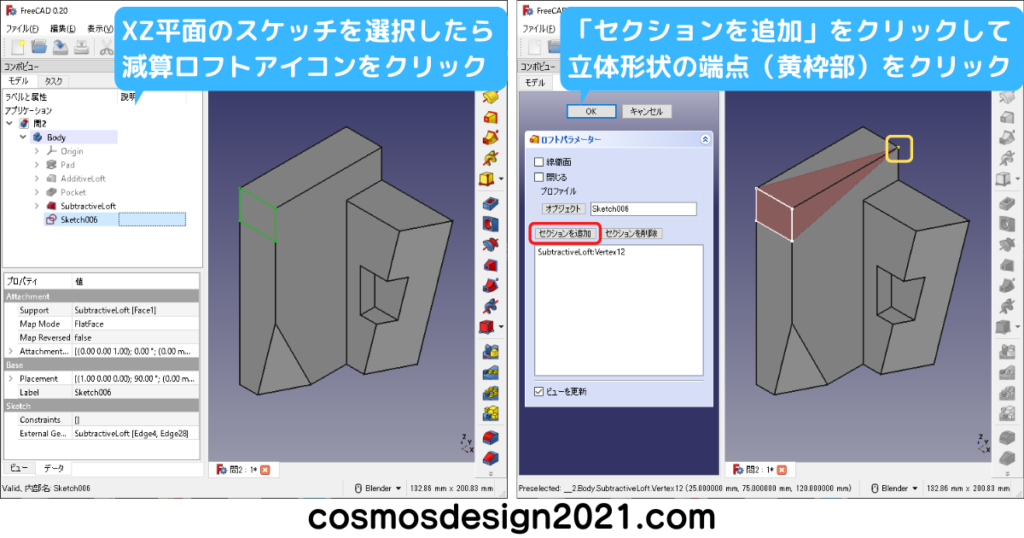
問5 第三角法の図面からモデリング
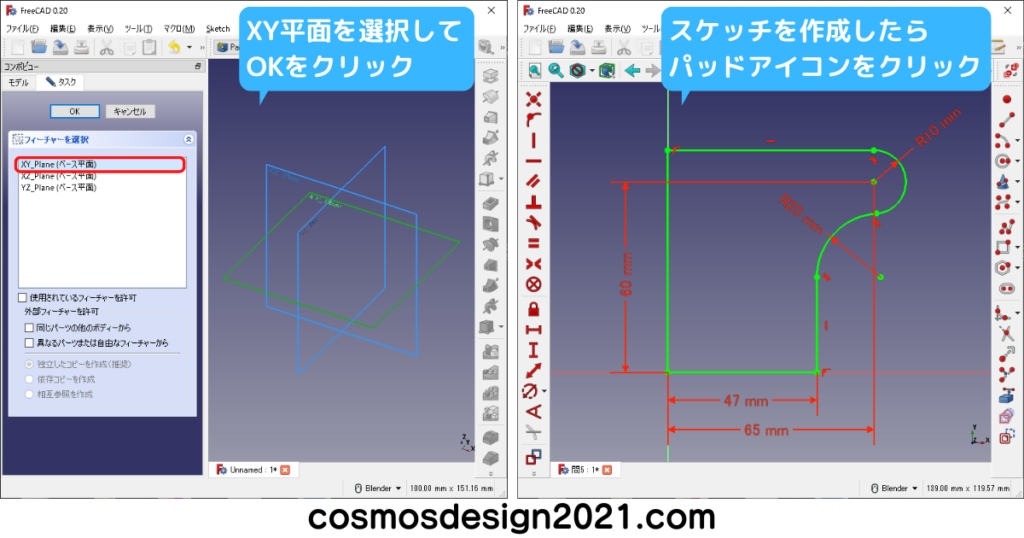
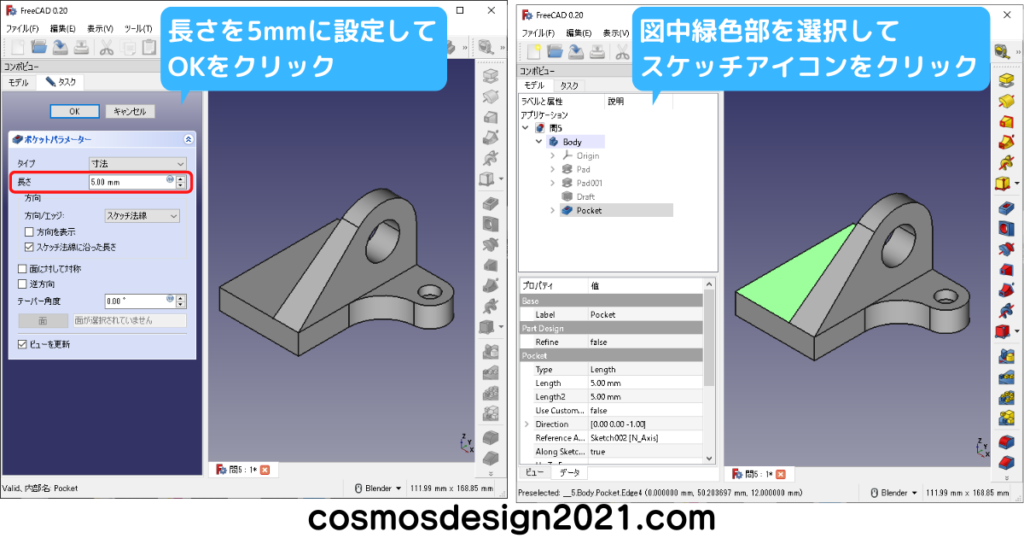
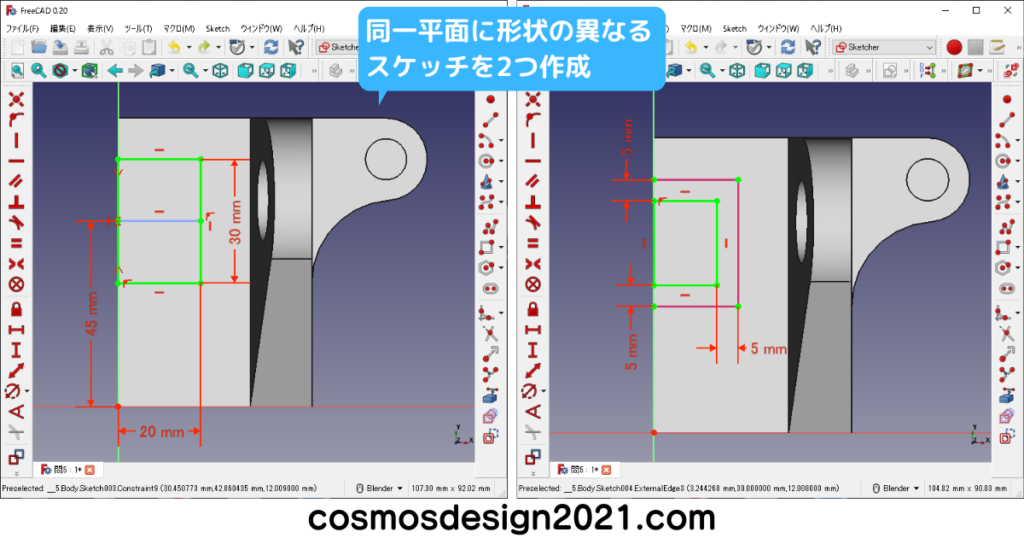
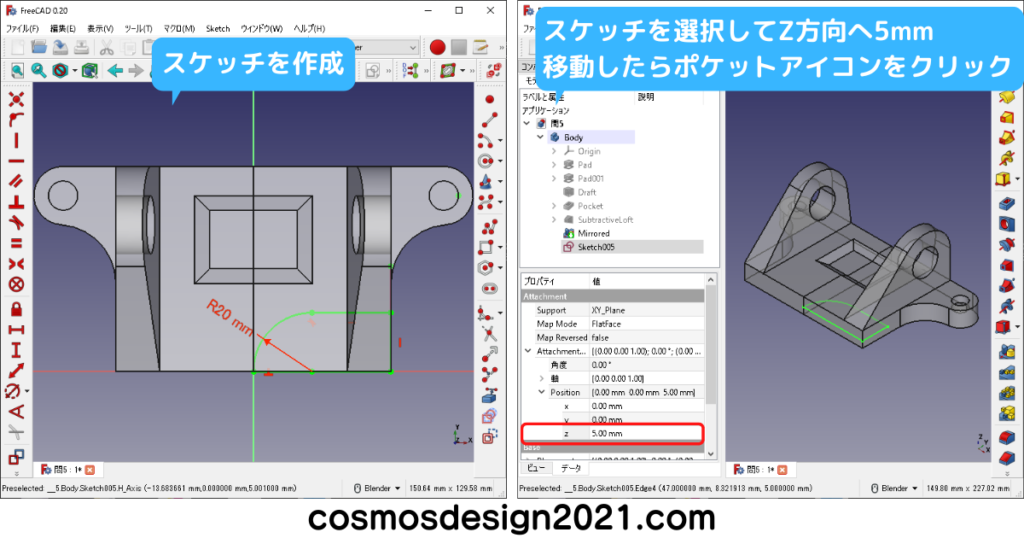
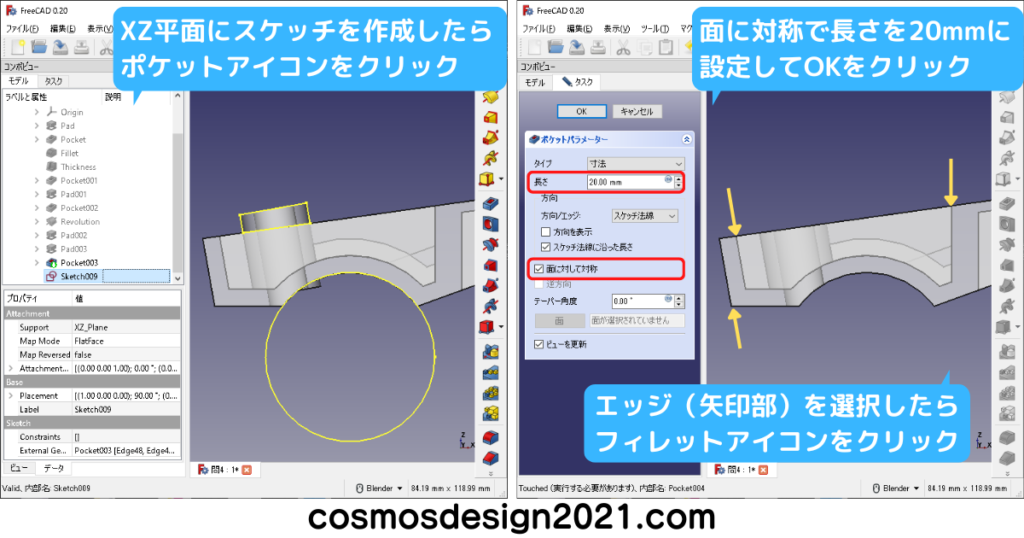
右下図のR20はPart Designワークベンチのフィレットでも作れます。
補足として、Part Designワークベンチのフィレットは、長さが18mmの面にR18のフィレットをかけると、エラーが発生してモデリングできません。（X軸方向の面の長さは65-47＝18mm）
エラーを回避する場合、R18から寸法を変更するか、右下図のように前もってスケッチでフィレットを作成しておきます。
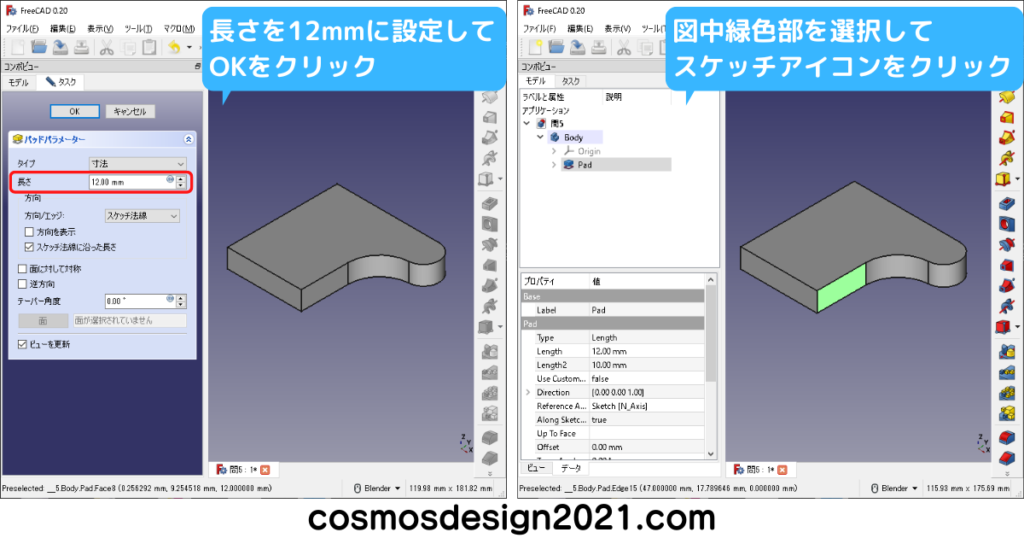
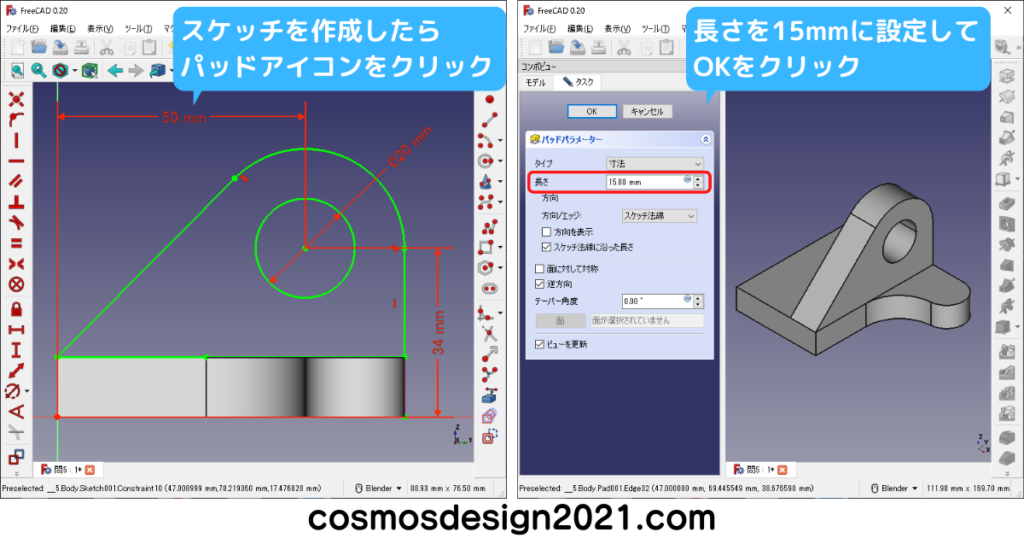
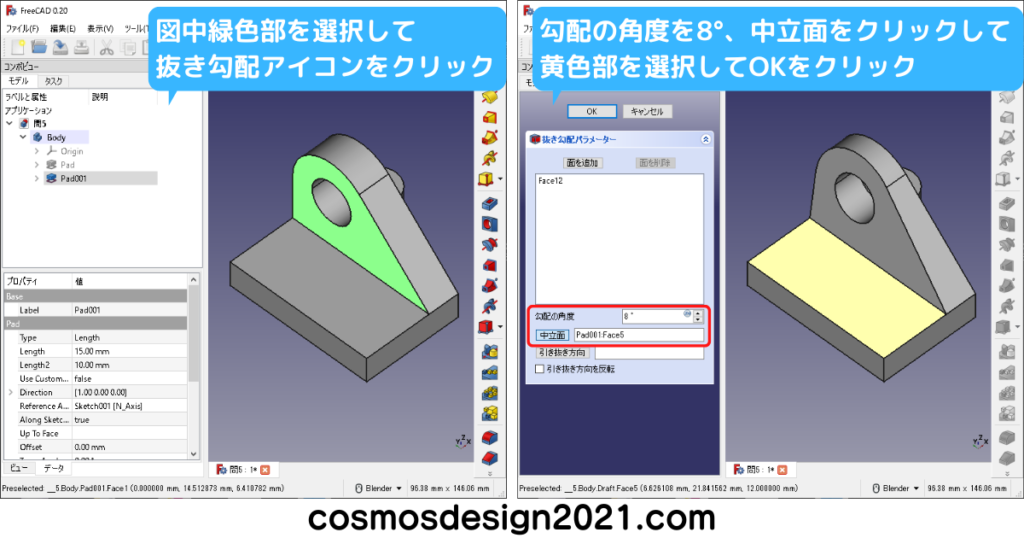
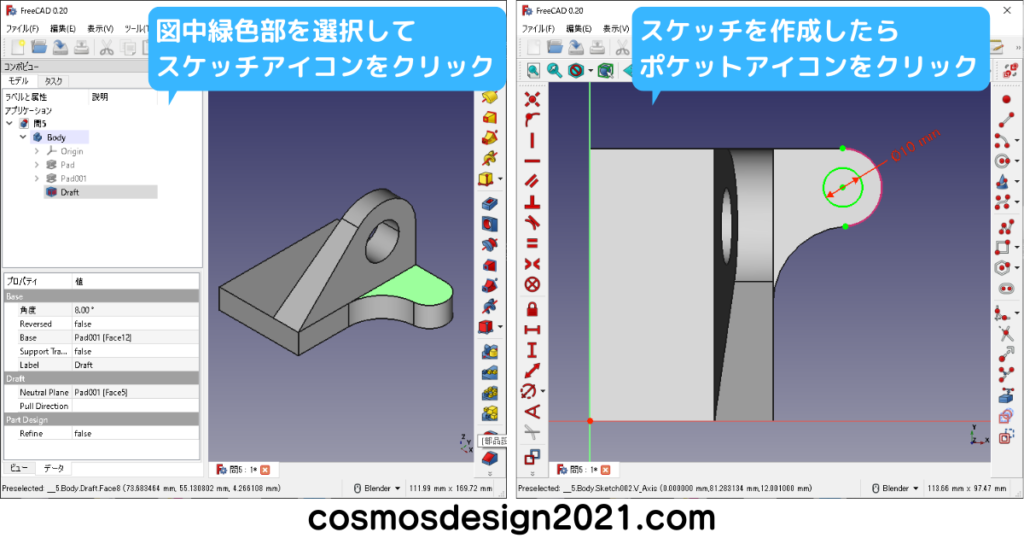
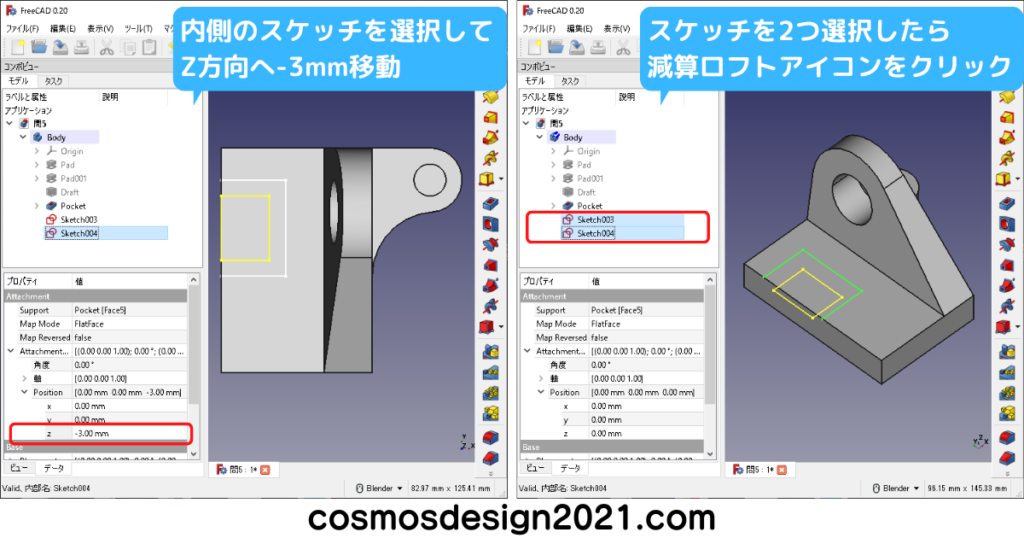
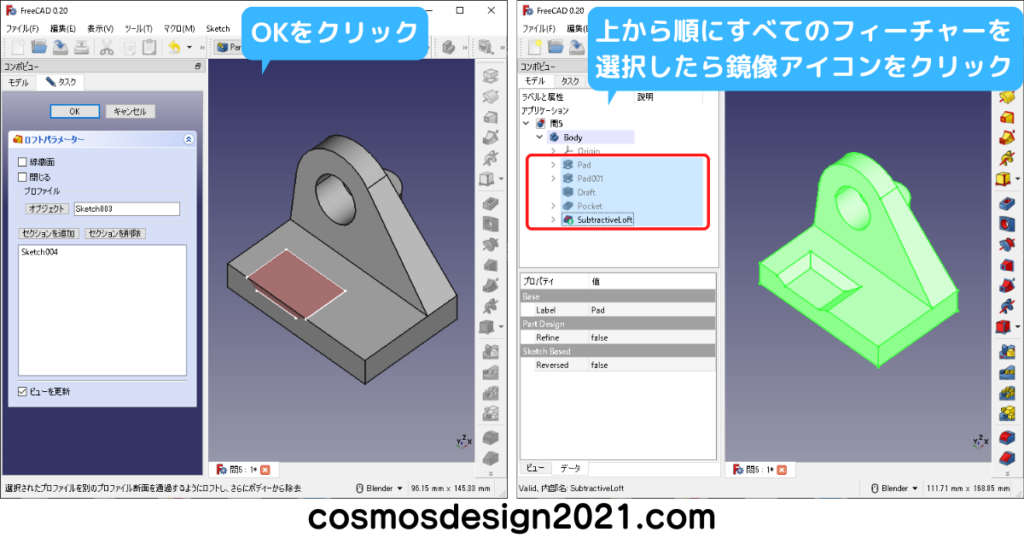
右下図のフィーチャーの選択順序を下から選択した場合、最後に作ったロフトがミラーリングされません。
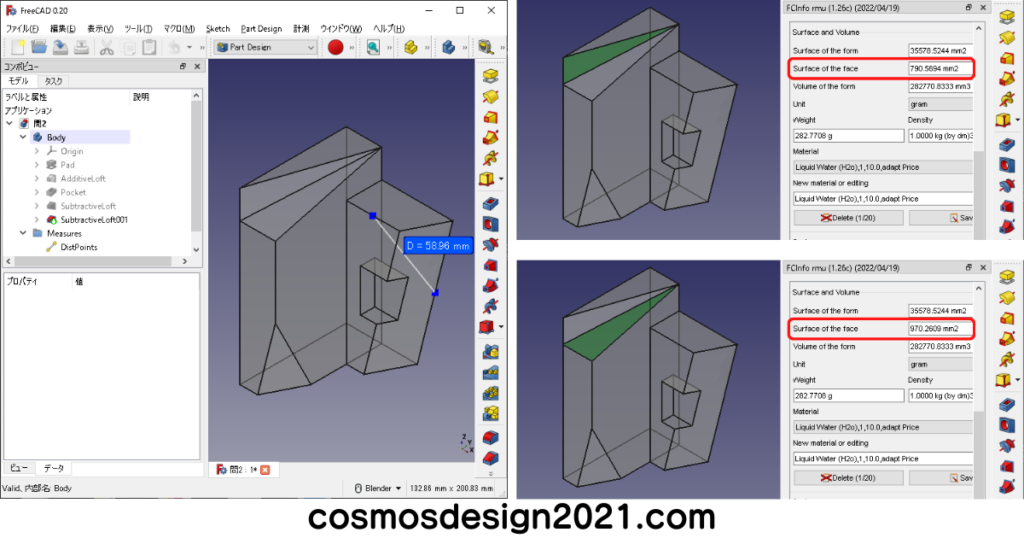
- 設問8の2点間距離は126.19mm よって解答は「1」
- 設問9の2点間距離は121.24mm よって解答は「3」
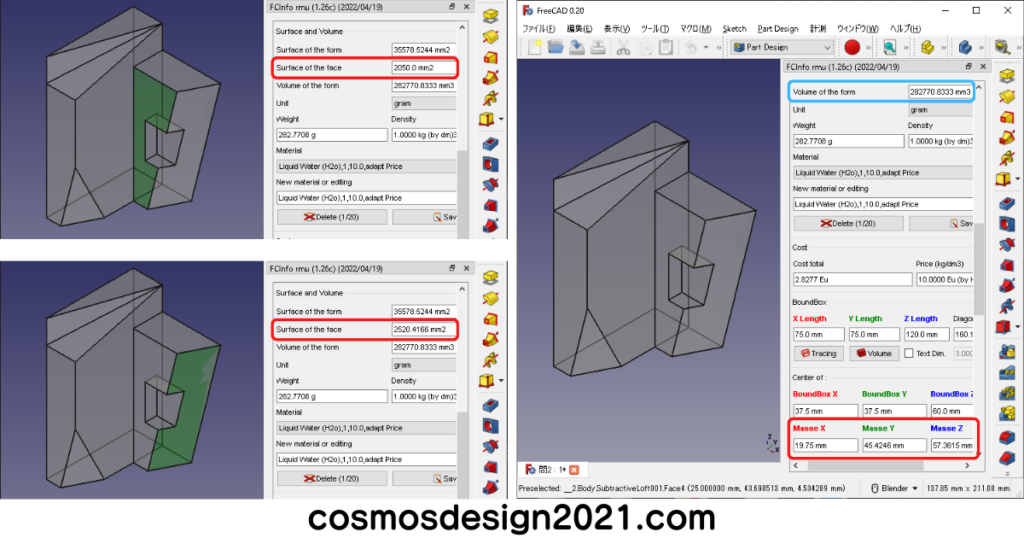
- 設問10の表面積は1672.5+748.2＝2420.7mm2 よって解答は「5」
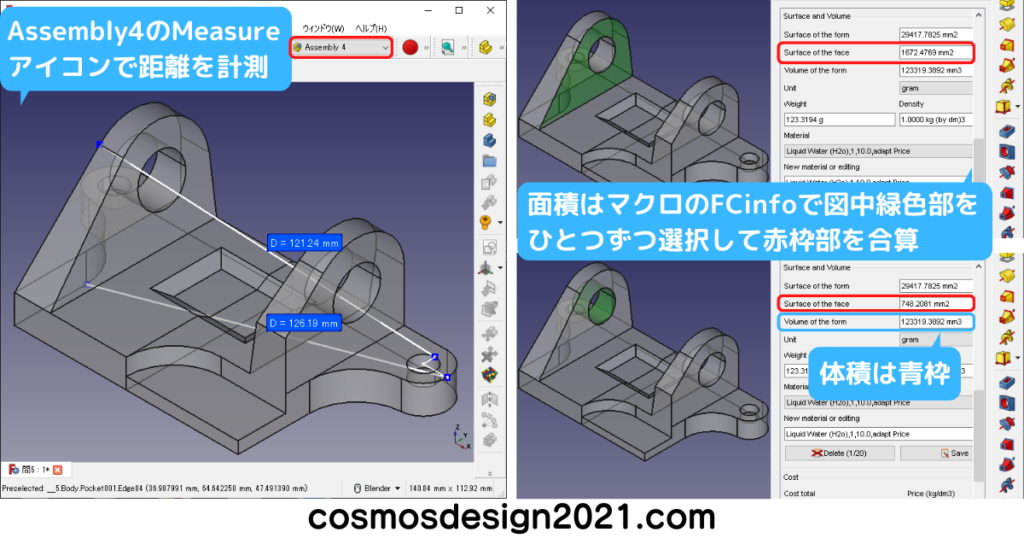
- 設問11の表面積は219.9+854.2+462.8＝1536.9mm2 よって解答は「5」
- 設問12の体積は123319mm3、重心座標はX：-2.150 Y：41.13 Z：12.52 よって解答は「2」
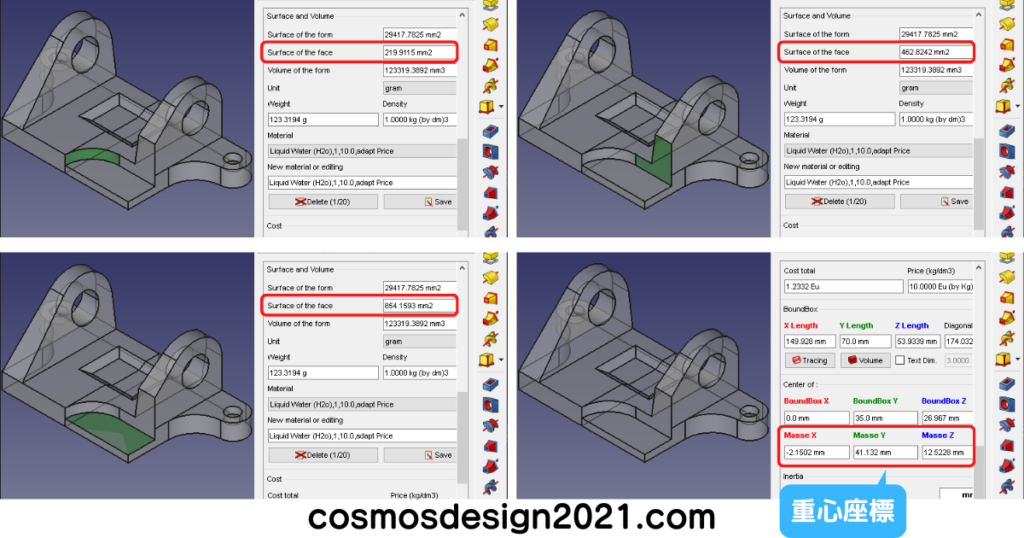
以上で問5は完了です。
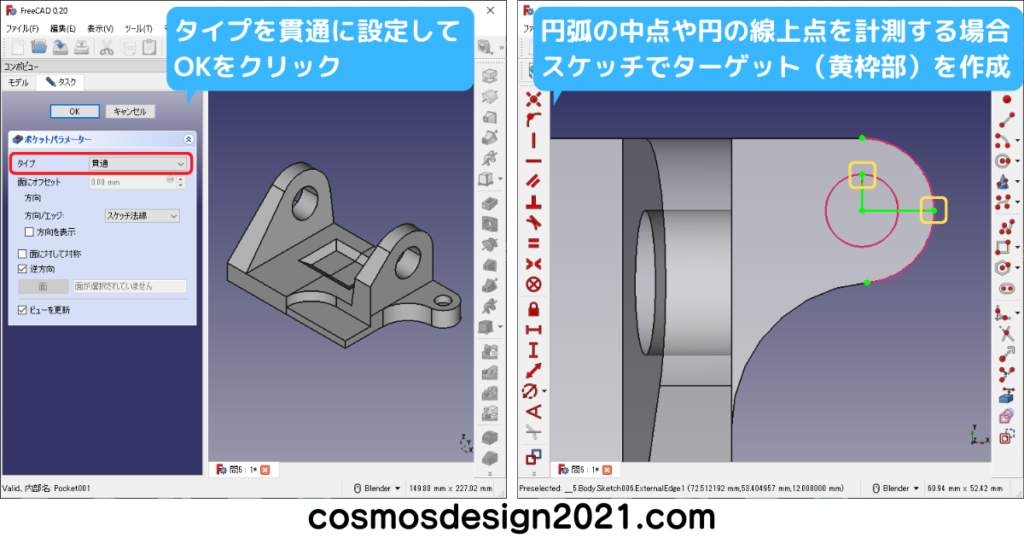
円弧の中点や円の線上点を2点間距離で計測する場合、スケッチでターゲットを作成しておきます。
これ以降の問は実際に挑戦してから見て欲しいので、スクロールしただけでは見られないようにしています。
問1 文章からモデリング
問1は口頭による指示を意識した文章問題のため、図面が読めなくても着手できますが、問題の指示を正確に捉えて、コマンドを使う必要があります。
直方体を作成します。（加算直方体で作成してもOK）
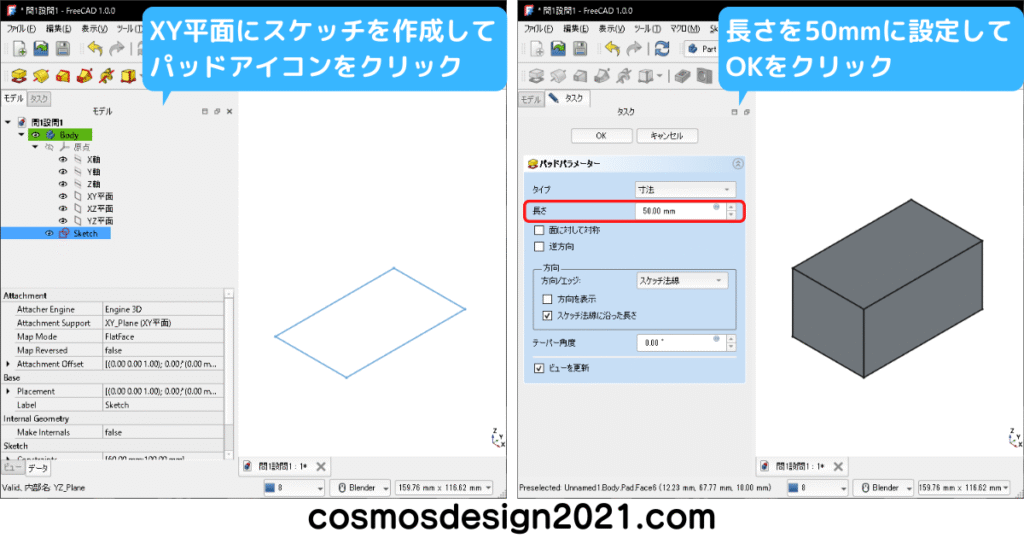
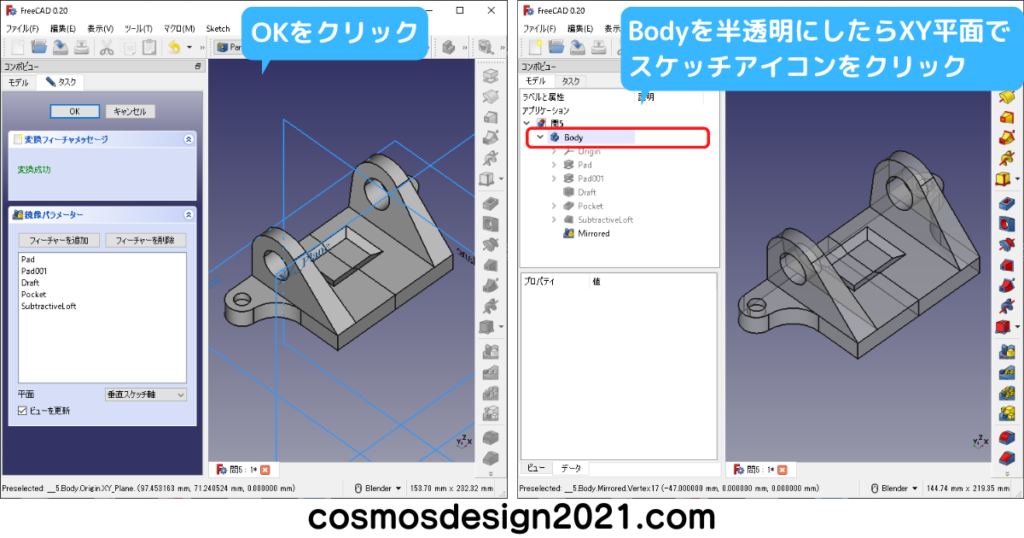
点を作成するとソリッドモデルに隠れてしまうため、解説ではBodyを半透明にします。
無限平面を作成します。
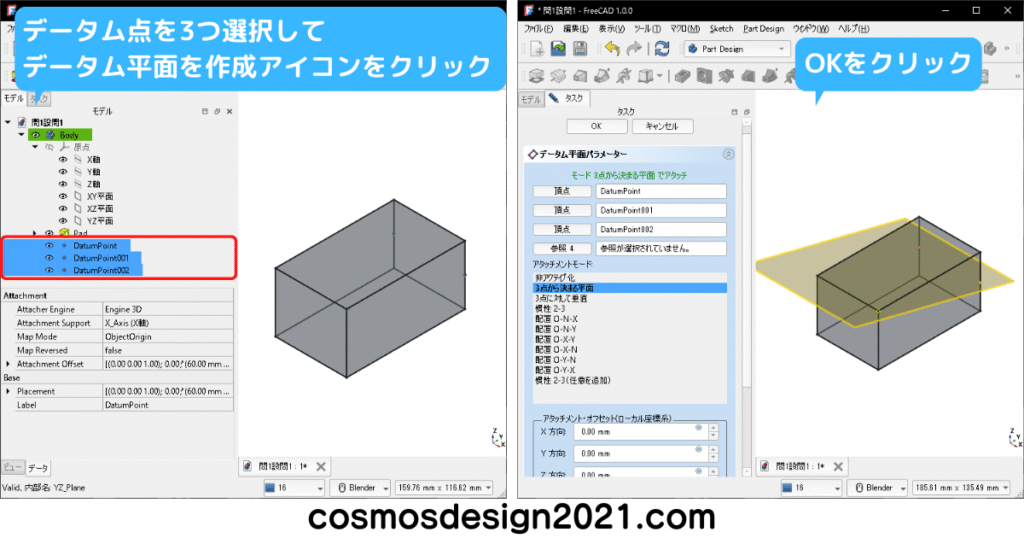
無限平面でソリッドモデルを切断して除去する場合、本来Partワークベンチのコマンドを使用すべきなのですが、円状パターンの複写元の形状として選択できなくなるため、ここではポケットで代用します。
ポケットのスケッチはソリッドモデルの外形よりも大きな枠で囲います。
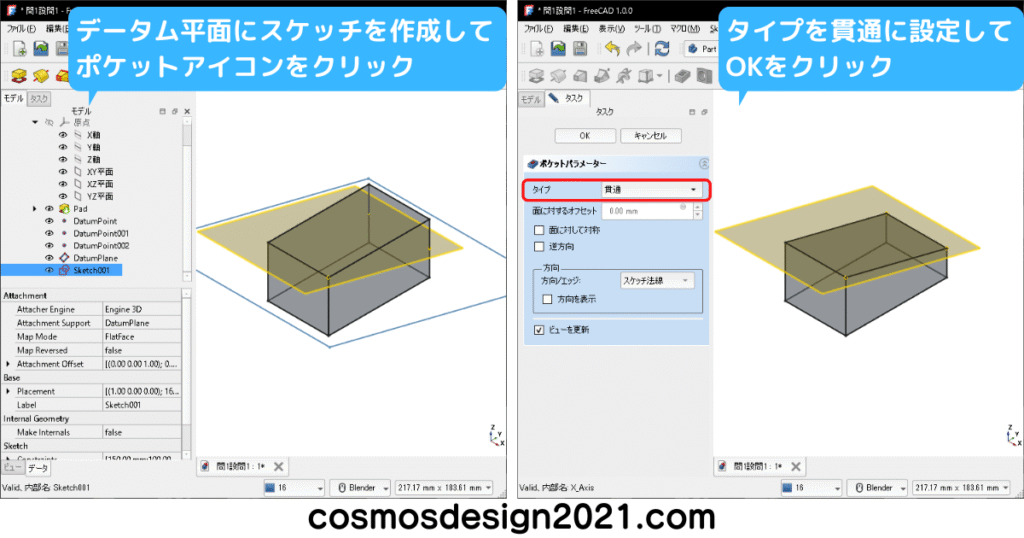
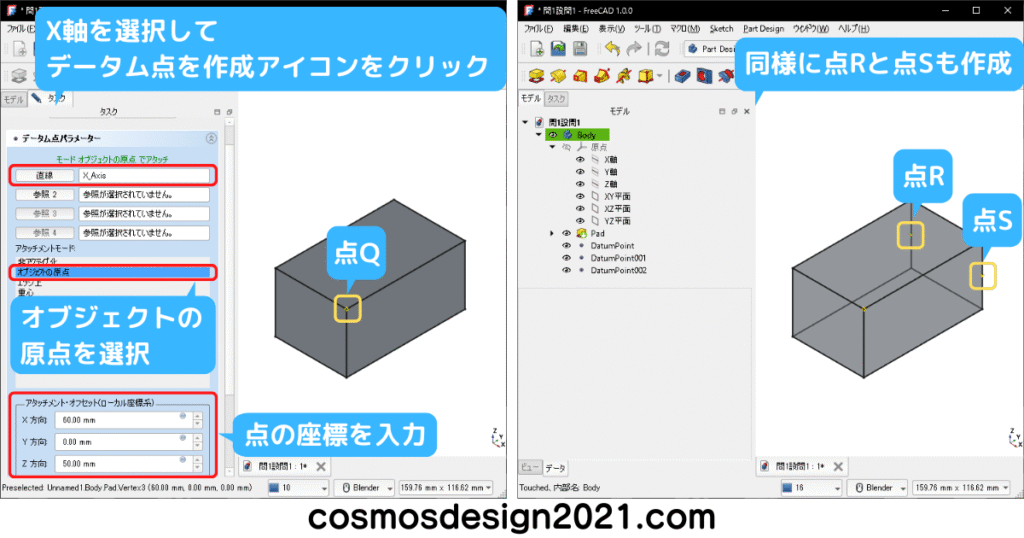
データム平面を非表示にして、2点と直線を作成します。
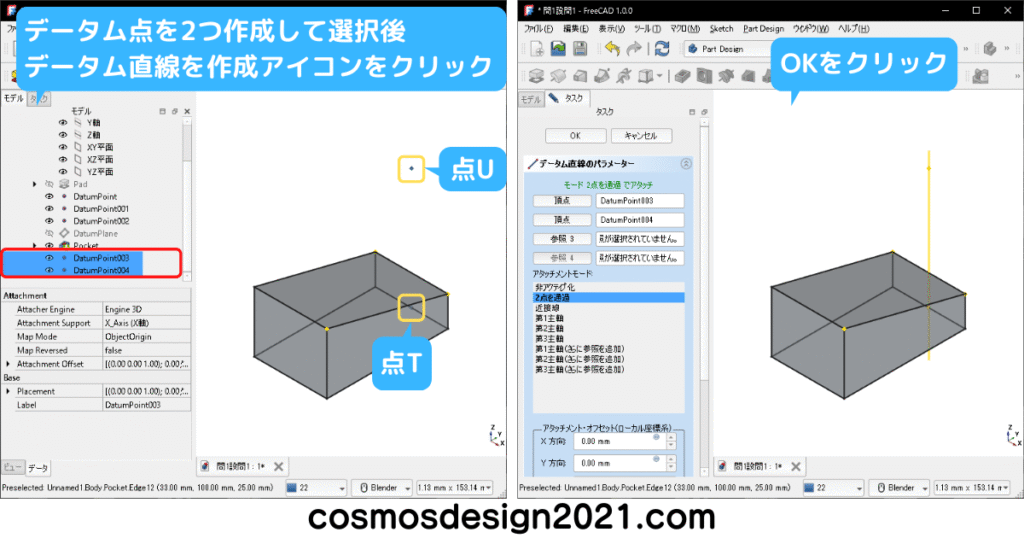
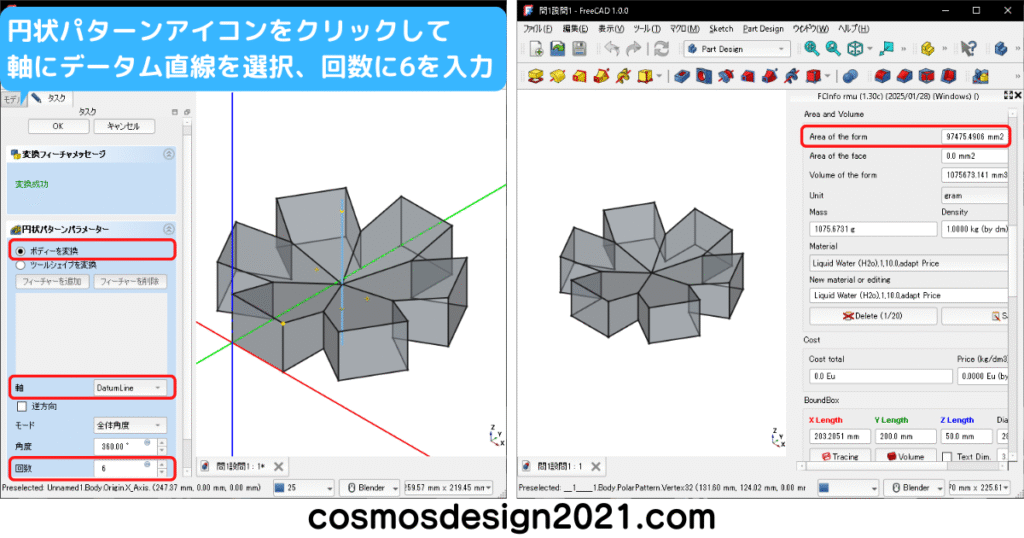
ソリッドモデルCと同様の形状を複写するため、「ボディーを変換」にチェックが入っていることを確認しておきます。
円状パターンを実行すると、複写後の形状は結合状態となります。
設問1の表面積は97475mm2 よって解答は「5」
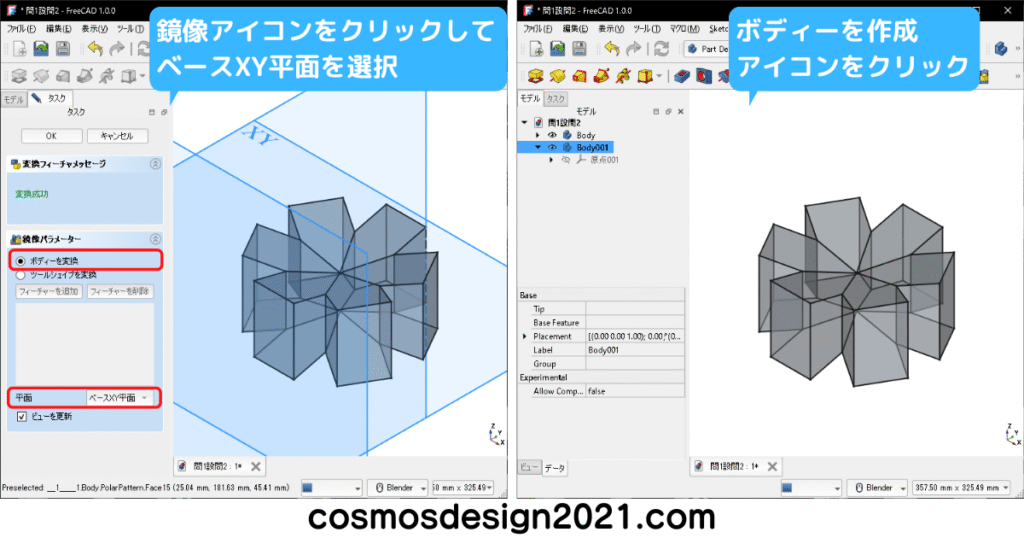
鏡像も複写後の形状は結合状態となります。
ブーリアン演算を実施する形状を作成するため、別のボディーを作成します。
球体を作成します。
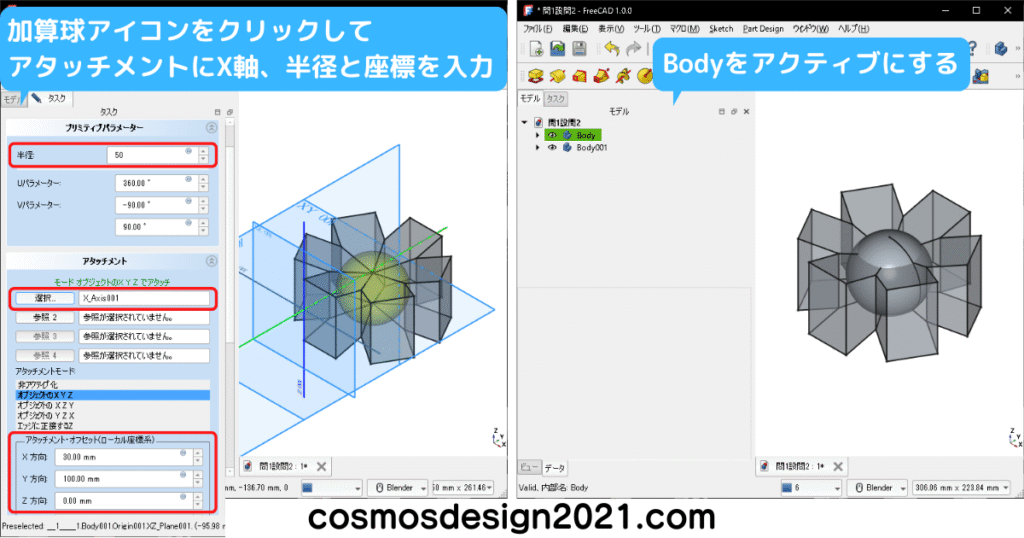
ソリッドモデルから球体を除去します。
設問2の表面積は154096mm2 よって解答は「1」
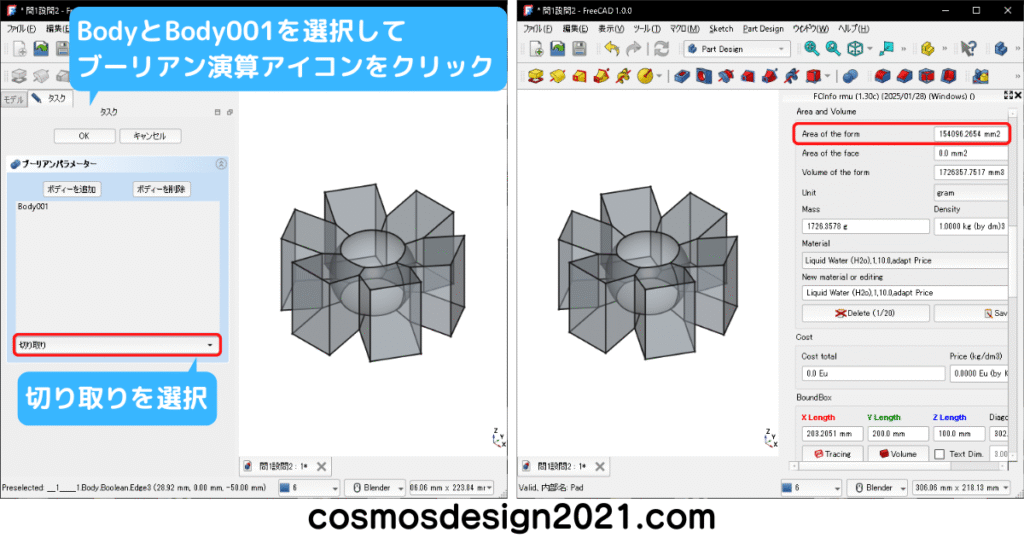
非表示にしておいたデータム平面を表示させます。
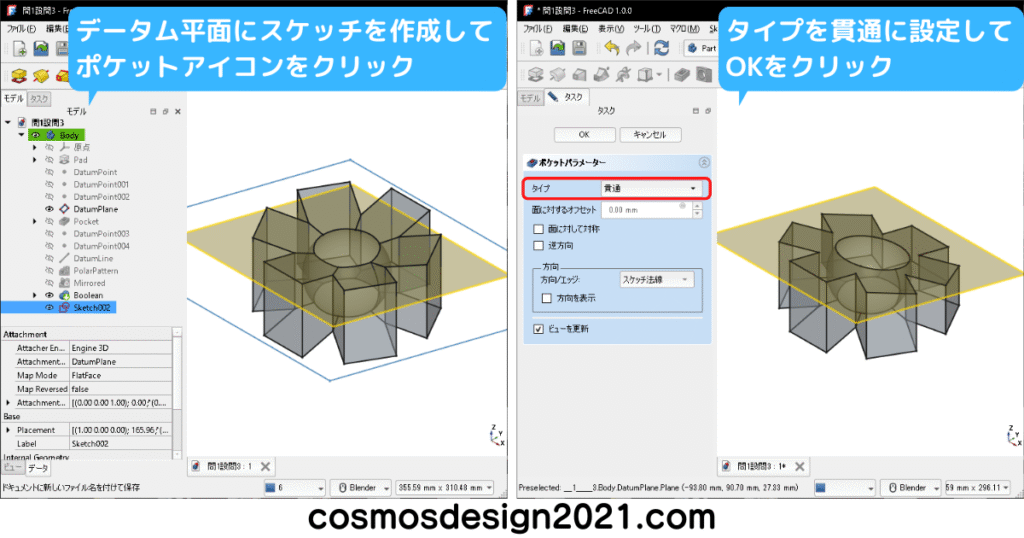
ブーリアン演算を実施する形状を作成するため、別のボディーを作成します。
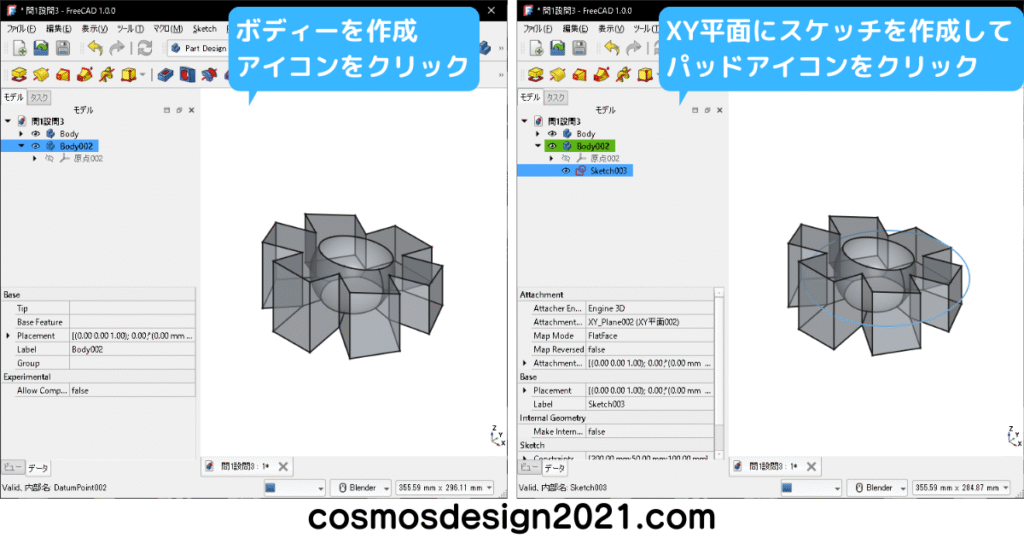
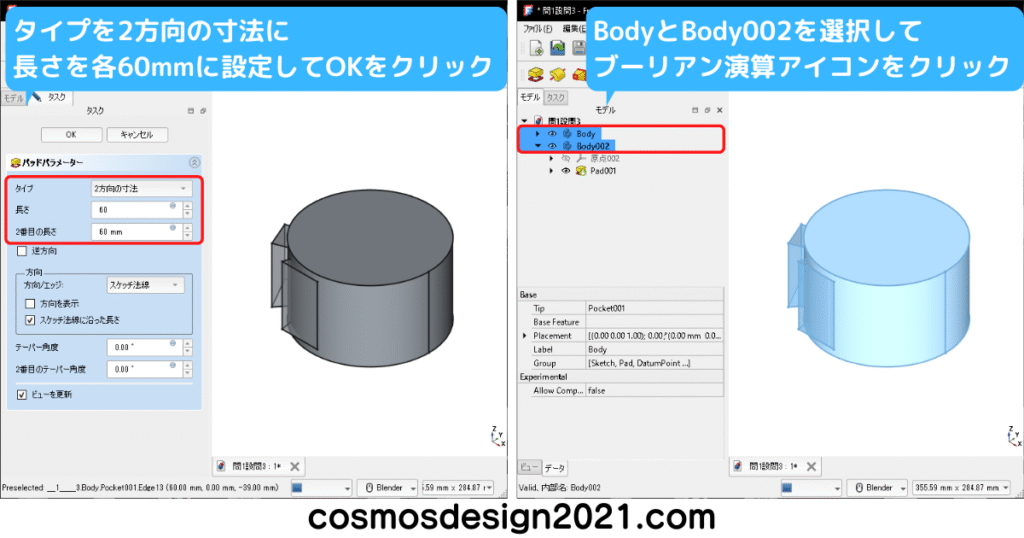
設問3の体積は1152842mm3、重心座標はX：42.03 Y：89.30 Z：-7.802 よって解答は「4」
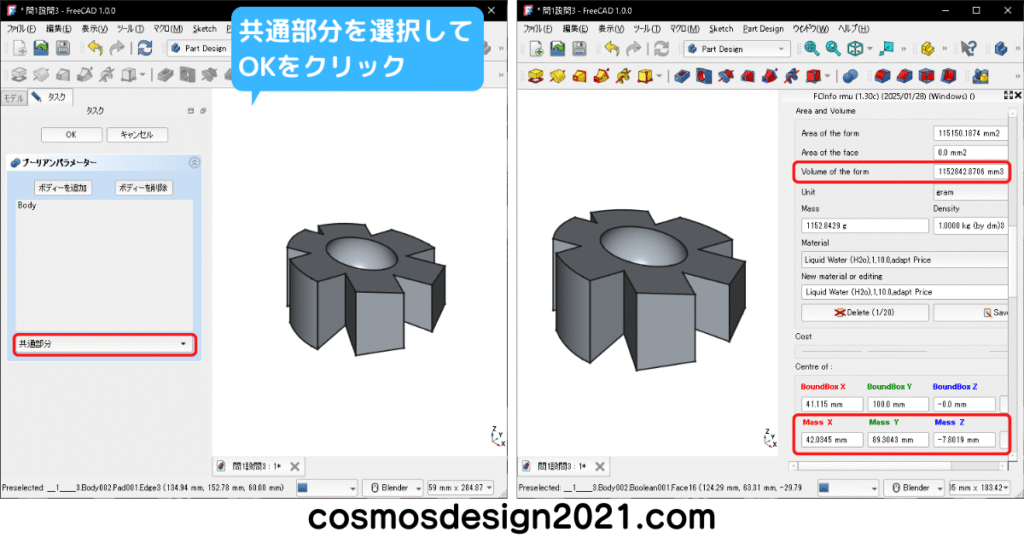
以上で問1は完了です。
ブーリアン演算を使用する場合、複数のBodyが必要になるため、問題文を先まで読んでおきます。
問2 第三角法の図面からモデリング
問2は図面から立体形状をイメージするのが難しいですが、粘り強く考えてみてください。
- 設問4の2点間距離は58.96mm よって解答は「4」
- 設問5の表面積は790.6+970.3＝1760.9mm2 よって解答は「5」
- 設問6の表面積は2050+2520.4＝4570.4mm2 よって解答は「2」
- 設問7の体積は282770mm3、重心座標はX：19.75 Y：45.42 Z：57.36 よって解答は「3」
以上で問2は完了です。
ロフトはスケッチの端点や立体形状の頂点を選ぶことで、三角錐や四角錘を作れます。
問3 作成したモデルのアセンブリ
問3はアセンブリの構築に重点を置いているため、図面から立体形状をイメージしやすく、モデリングの難度も低めです。
設問8と設問9の解説は割愛するので、自力でモデリングしてみてください。
- 設問8の体積は172005mm3、重心座標はX：53.57 Y：40.05 Z：29.44 よって解答は「1」
- 設問9の体積は256939mm3、重心座標はX：25.38 Y：45.98 Z：40.35 よって解答は「3」
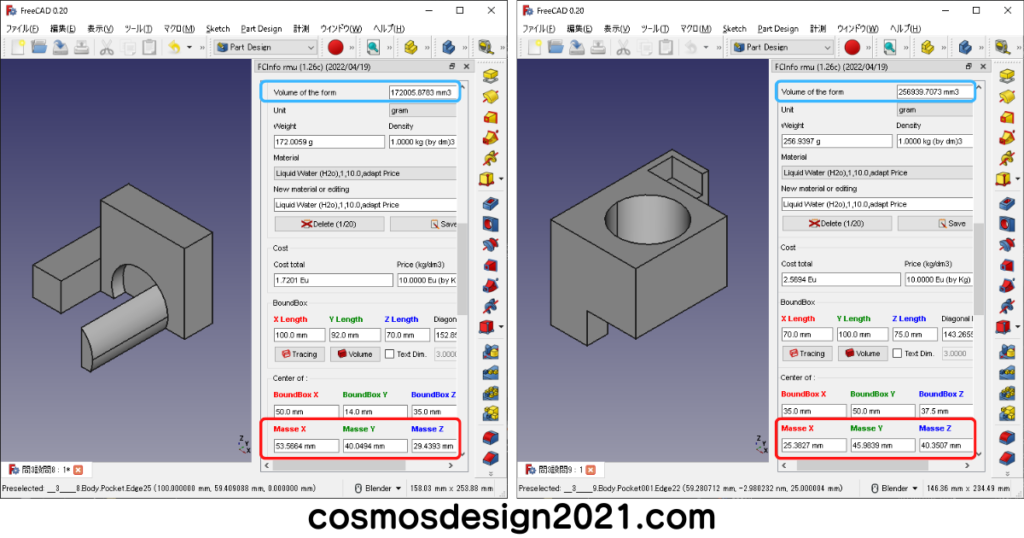
設問8で作成したモデルを開いたら、メニューバーの「ファイル」→「プロジェクトの統合」を選択して、設問9で作成したモデルを読込みます。
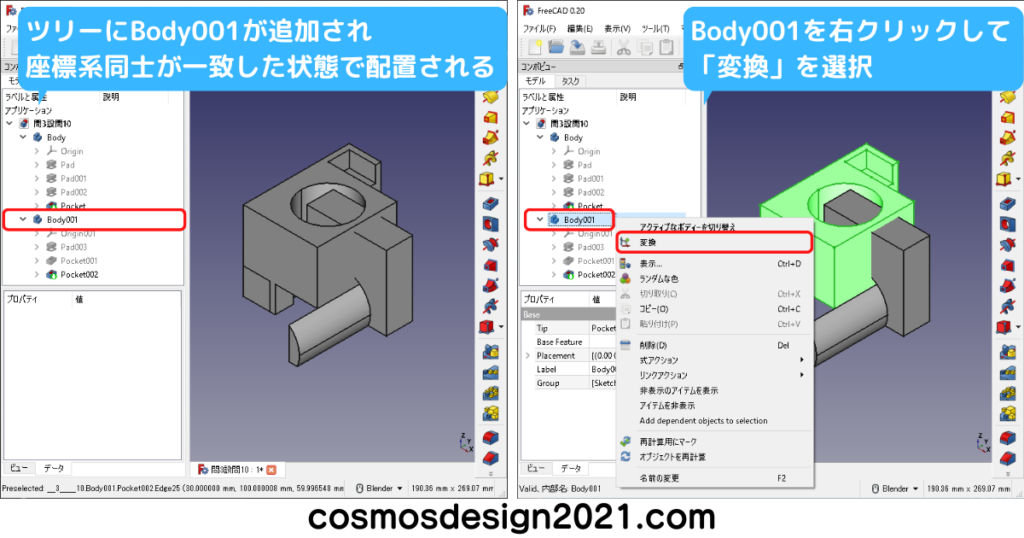
Body001に座標系が表示されるので、黄枠部（軸方向移動）と赤枠部（回転方向移動）をドラッグして、目的の位置へ移動させます。
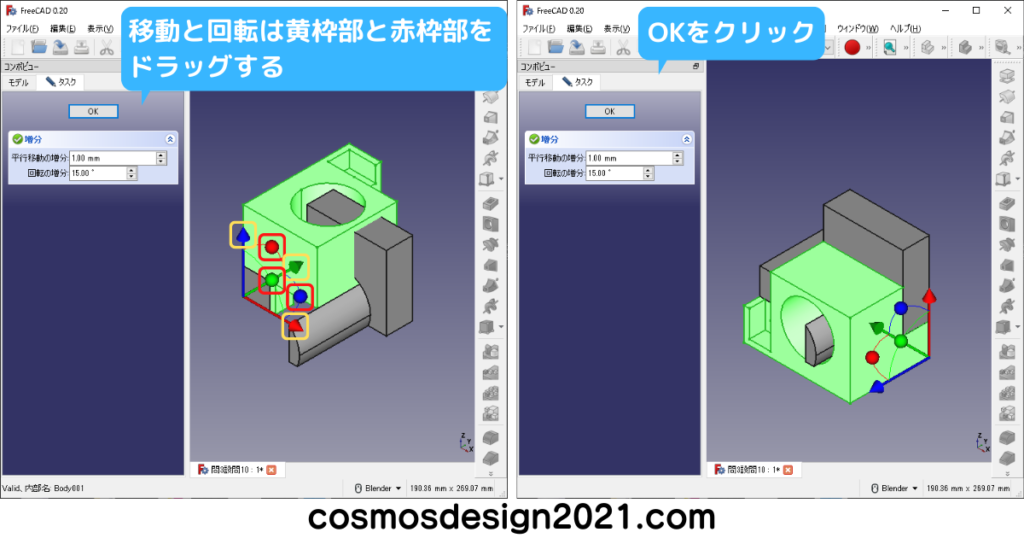
設問10の重心座標はX：53.84 Y：27.83 Z：9.039 よって解答は「3」
設問11と設問12の解説は割愛するので、自力でモデリングしてみてください。
- 設問11の体積は243337mm3、重心座標はX：37.09 Y：51.75 Z：19.98 よって解答は「2」
- 設問12の体積は241474mm3、重心座標はX：41.60 Y：54.03 Z：21.60 よって解答は「4」
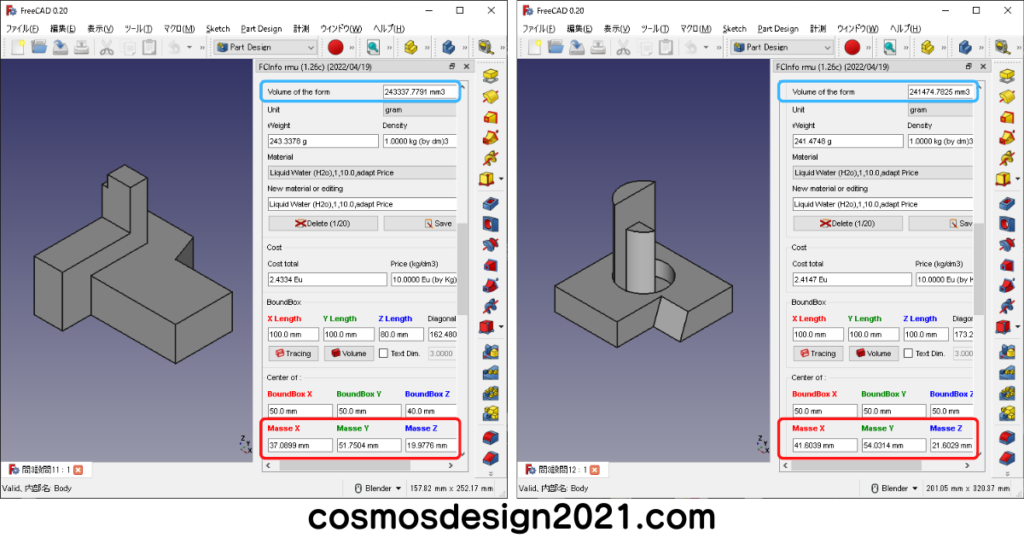
設問10で作成したアセンブリを開いたら、設問11と設問12で作成したモデルを読込みます。
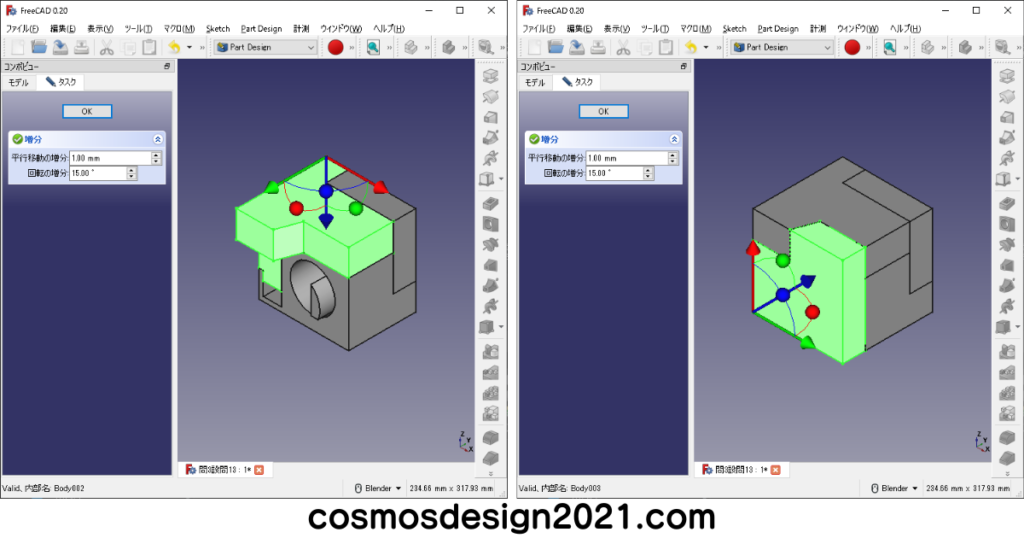
設問13の重心座標はX：49.43 Y：10.40 Z：20.63 よって解答は「2」
以上で問3は完了です。
アセンブリの重心座標は、プロジェクトの統合で複数のBodyを読込んでから、ブーリアン演算で結合して求めます。
本来、AssemblyワークベンチやAssembly4ワークベンチで、アセンブリを組んで重心座標を求めたかったのですが、Part DesignのメジャーやFCInfoではアセンブリの重心座標を求められなかったため、上記の代替え案で求めました。
問4 第三角法の図面からモデリング
問4は図面から立体形状をイメージしやすいですが、どの順序でモデリングしていくか考える必要があります。
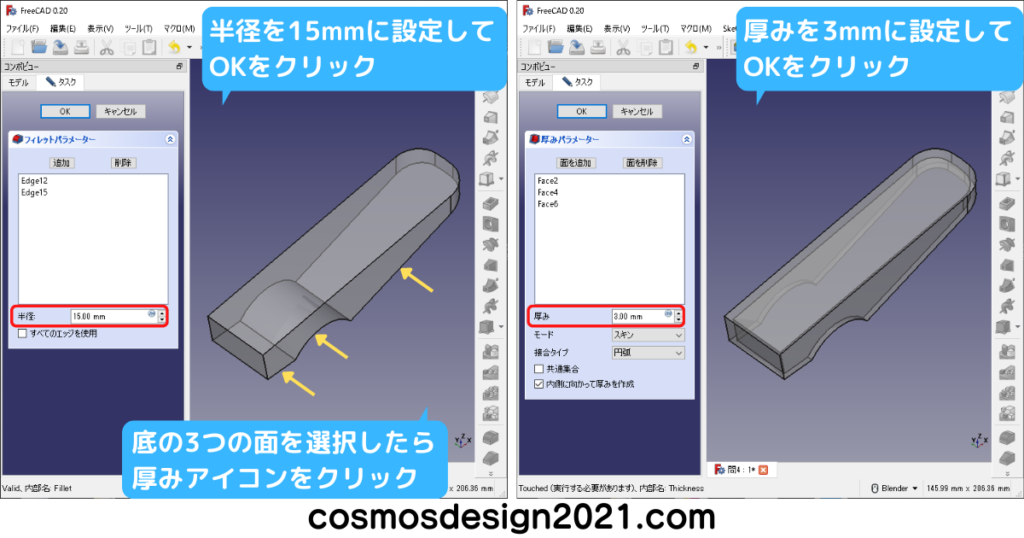
この問いは色々な方法でモデリングできますが、過去問を見る限り、厚み（シェル）を使う問と言えます。
まずは図面を見て肉厚が一定となる範囲を確認してから、シェルを使うタイミングを考えておきます。
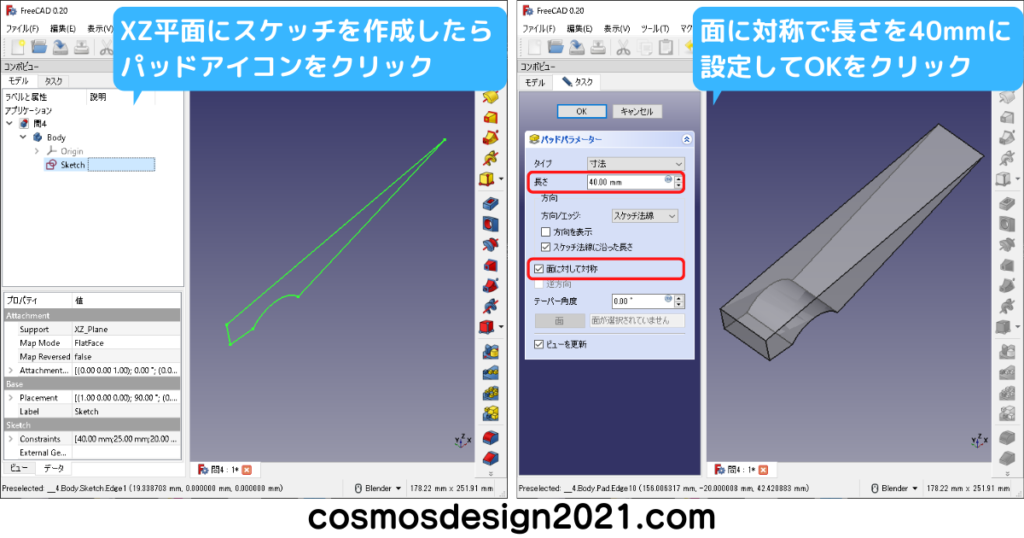
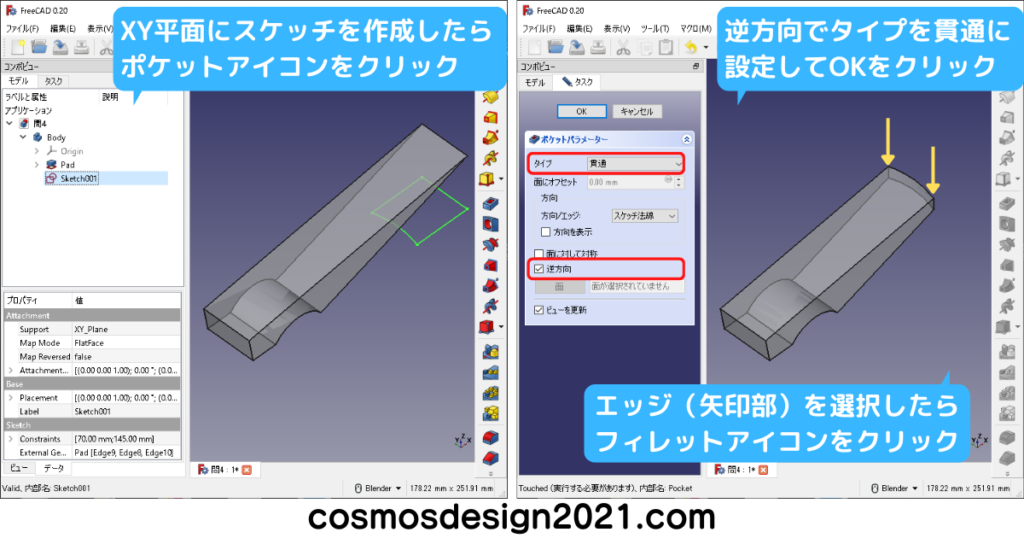
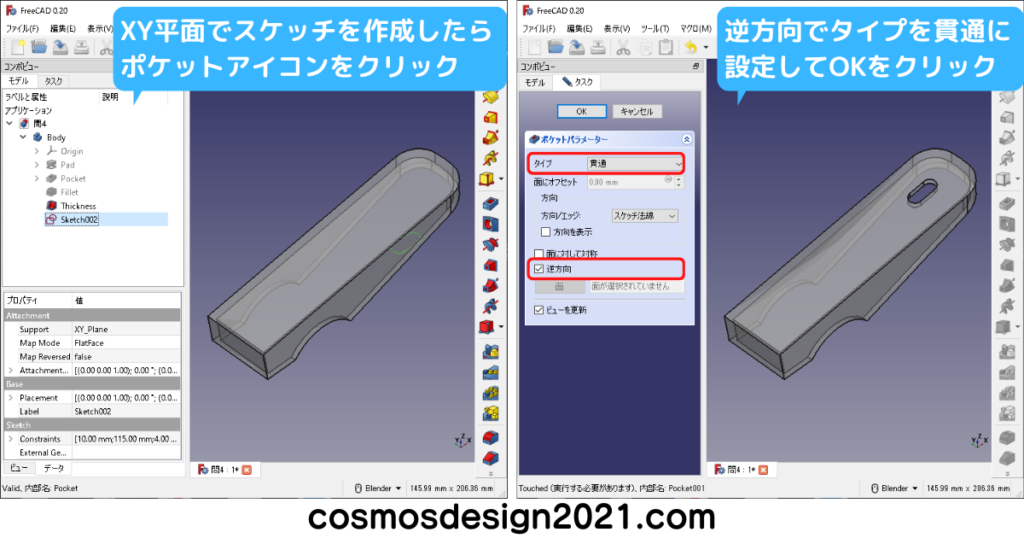
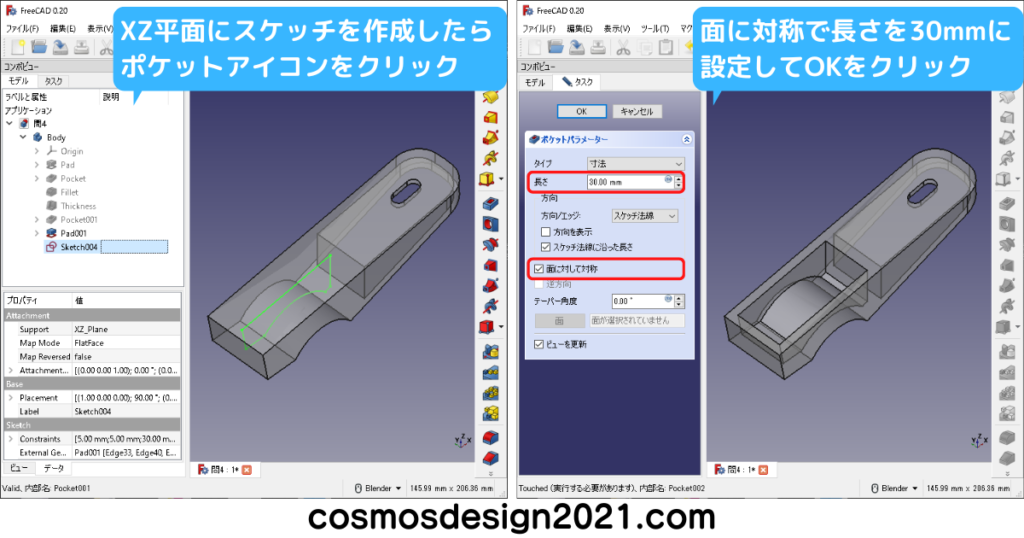
左下図はXY平面に長穴のスケッチを作成しました。
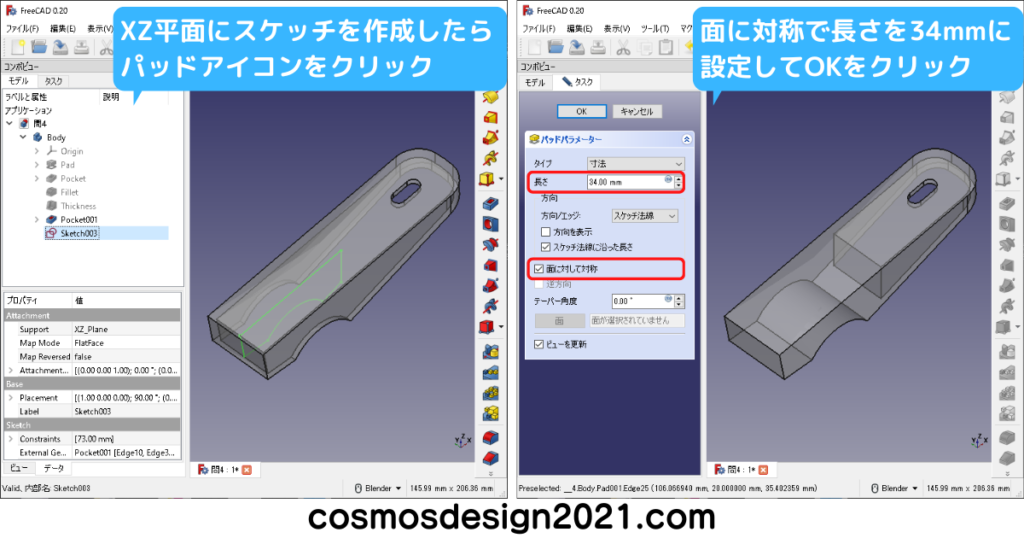
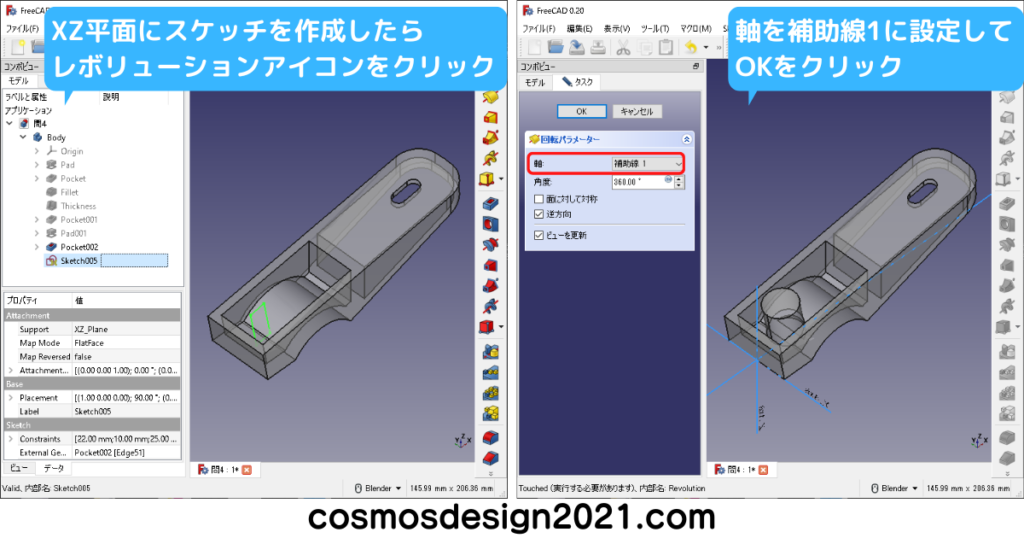
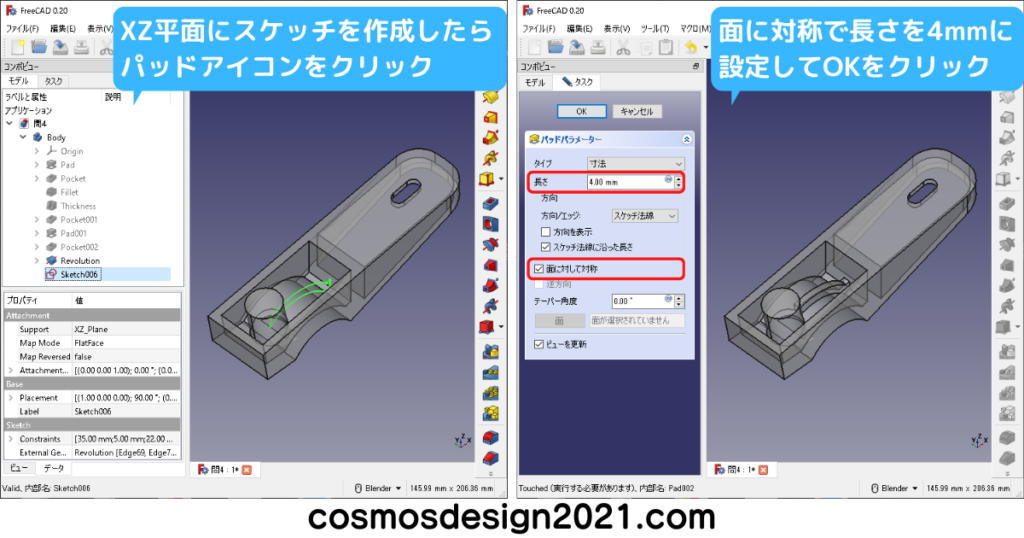
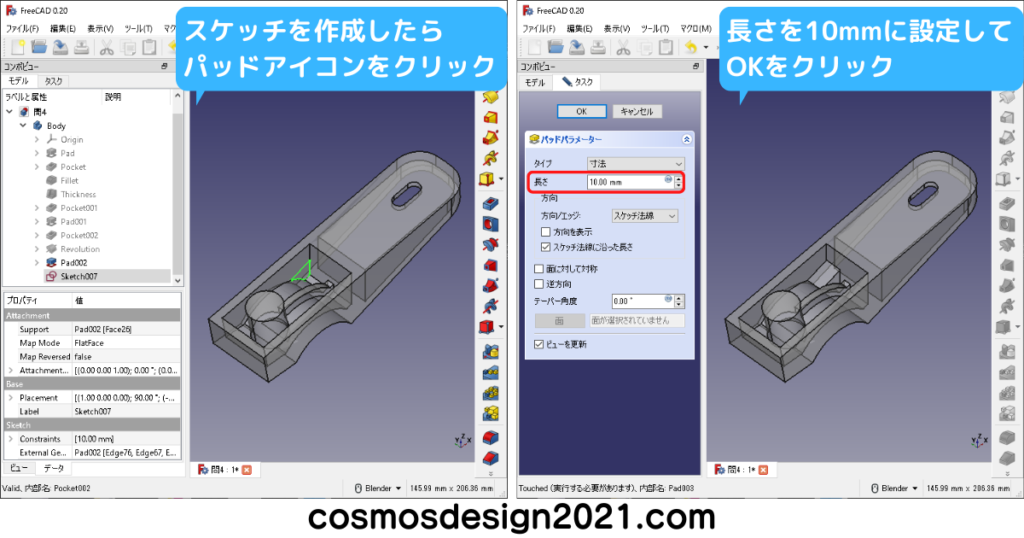
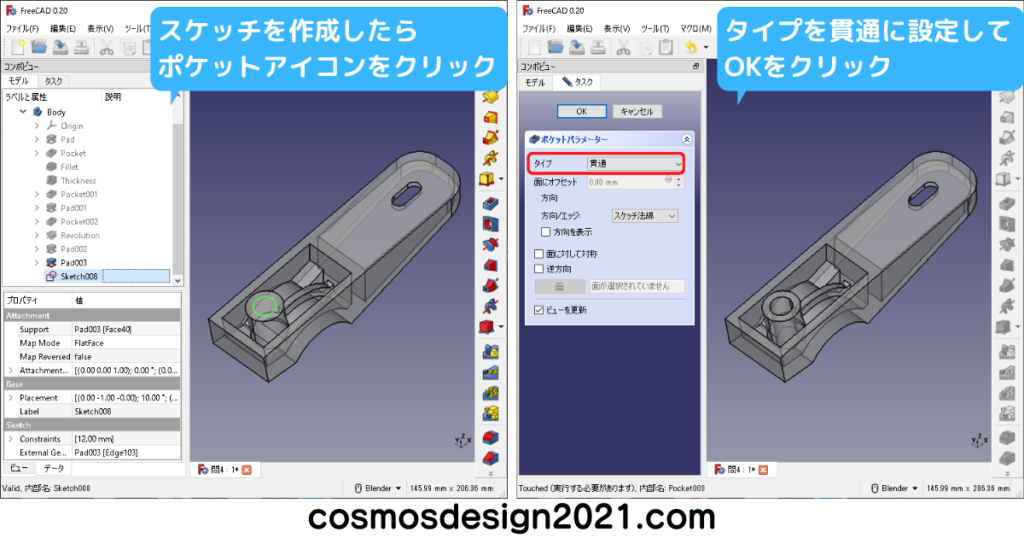
設問14の表面積は1102mm2 よって解答は「5」
- 設問15の2点間距離は133.3mm よって解答は「2」
- 設問16の表面積は140.2mm2 よって解答は「4」
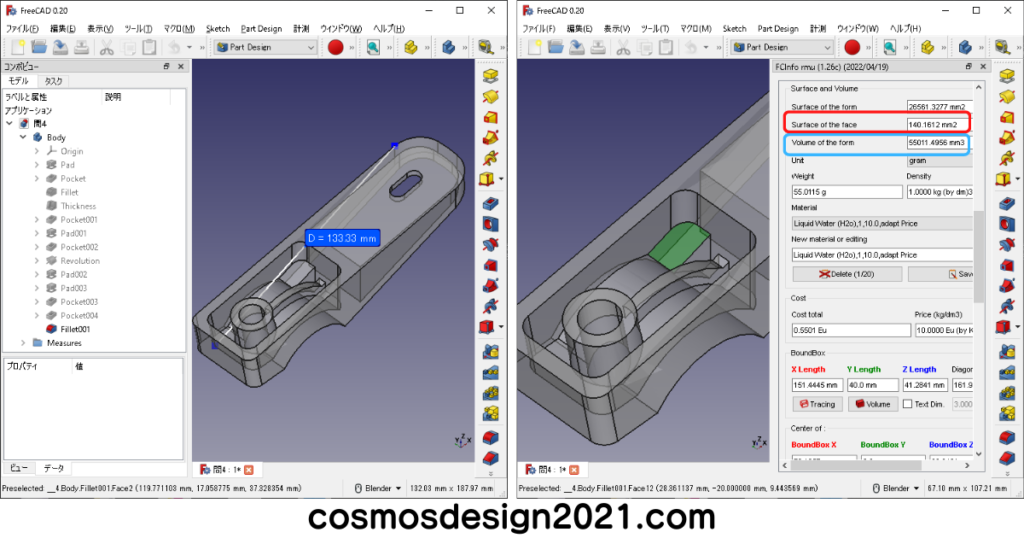
- 設問17の表面積は142.8+307.4+9.7＝459.9mm2 よって解答は「1」
- 設問18の体積は55011mm3、重心座標はX：58.05 Y：0.142 Z：17.75 よって解答は「1」
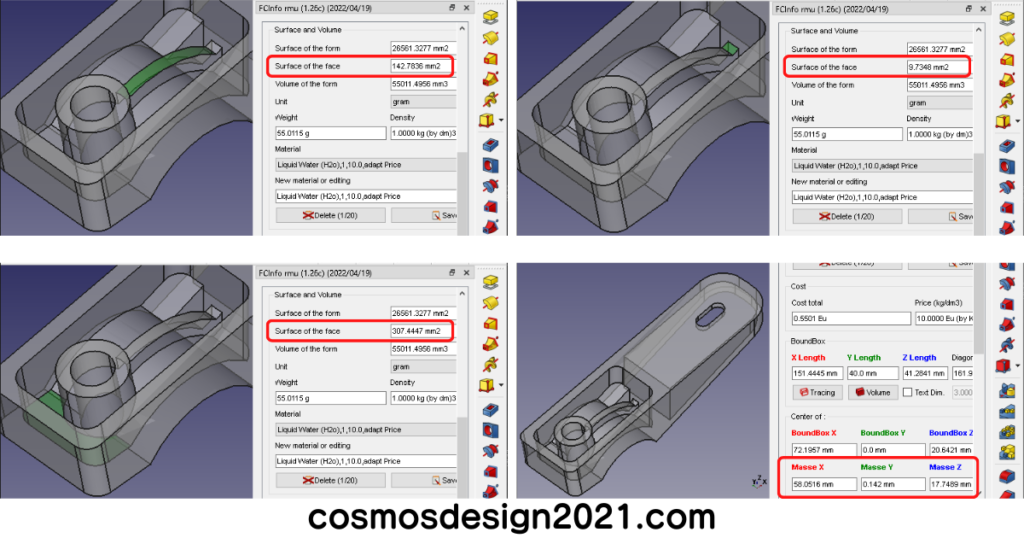
以上で問4は完了です。
どの順序でモデリングしていくかザックリと決めておくと、トータルの作業時間を短くできます。これは練習を重ねていくと顕著に現れるので、考える癖をつけましょう。
まとめ｜FreeCAD 練習問題｜3次元CAD利用技術者試験のサンプル問題を解説
モデリングの基本的な使い方を学習した方は、実際に問題を通して理解度を深められたと思います。
難しく感じたり、スムーズに操作できなかった場合は、この記事を繰り返し読んで練習してみてください。
各問題にはモデリング目標時間が記載されているので、高みを目指す方はモデリング時間を計測してみてください。
CADは繰り返し使うことで操作スピードが早くなるので日々精進です！
練習問題を解き終えたら
練習問題を解き終えて、これだったらできるかも！？モデリングスピードを早くしたい！自信を付けたい！3次元CADの資格が欲しい！資格手当が欲しい！という方は、下記の記事に進んでください。
